Pythagoras Theorem

Pythagoras Theorem

• In a right angled triangle the square of the long side is equal to the sum of the squares of the other two sides.
  
  
  
  It is stated in this formula:
  
  
  If we know the lengths of two sides of a right angled triangle, we can find the length of the third side. (But remember it only works on right angled triangles!) 
• Note:  
• a is the longest side of the triangle 
•   b and c are the other two sides
  
  
  
  
  There are certain sets of numbers that have a very special property in relation to the Pythagorean Theorem.  Not only do these numbers satisfy the Pythagorean Theorem, but any multiples of these numbers also satisfy the Pythagorean Theorem.  
  
  
  
  

  

  For example:  the numbers 3, 4, and 5 satisfy the Pythagorean Theorem.  If you multiply all three numbers by 2  (6, 8, and 10), these new numbers ALSO satisfy the Pythagorean theorem.  
    The special sets of numbers that possess this property are called
  Pythagorean Triples.
  
  
  The most common Pythagorean Triples are:
  3, 4, 5
  5, 12, 13
  8, 15, 17

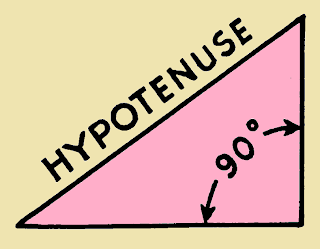
Hypotenuse

What is Hypotenuse?

•  Hypotenuse is the longest side of the triangle.

•  Hypotenuse is the side opposite the right angle in a right angled triangle. 

Determine the Hypotenuse

From this figure, we can see that c is the side opposite right angle.

So,  C = HYPOTENUSE 



Calculate the Hypotenuse


Look at the triangle below.

We want to find the length of the hypotenuse (h).

 Pythagoras' Theorem tells us:

 The square of the hypotenuse is equal to the sum of the squares of the two shorter sides.
In this case, this means that h² is equal to 5² + 12².

So the length of the hypotenuse (h) can be worked out as follows:

h² = 5² + 12²    ( work out the squares of the two shorter side )
h² = 25 + 144   (add the squares of the two shorter sides together )
h² = 169           ( square root both sides to find the value of h)
h  = 13

We can now see that the length of the hypotenuse (h) is 13m.