Courseware

Games

You can click to this link to start your game :

http://www.math-play.com/Pythagorean-Theorem-Jeopardy/Pythagorean-Theorem-Jeopardy.html

http://www.kidsnumbers.com/pythagorean-theorem-game.php

http://www.math-play.com/Pythagorean-Theorem-Game.html

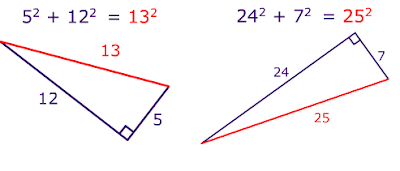
What is Pythagoras Theorem ??

The Pythagoras Theorem or Pythagorean Theorem, named after the Greek mathematician Pythagoras states that :

" In any right triangle, the area of the square whose side is tje hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle). "

This is usually summarized as follows :

" The square of the hypotenuse of a right triangle is equal to the sum of the squares on the other two sides. "

If we let c be the length of the hypotenuse and a and b be the lengths of the other two sides, the theorem can be expressed as the equation :

This equation provides a simple relation among the three sides of a right triangle so that if the lengths of any two sides are known, the length of the third side can be found. A generalization of this theorem is the law of cosines, which allows the computation of the length of the third side of any triangle, given the lengths of two sides and the size of the angle between them. If the angle between the sides is a right angle it reduces to the Pythagorean Theorem.

EXAMPLE EXERCISE

1.Which side is the hypotenuse in the right-angled triangles below ?

The answer is C

Because we know that hypotenuse is the side opposite the right angle in a right angled triangle.  

2.  Calculate the length of the hypotenuse 

c = 8  and  b = 4.  What is a?

We know c² + b² = a²

We want to find a.

so,  let c = 8 and  b = 4.

So c2 = 64    

b²  = 16

 a²  = 64  + 16

      =   80

Then, a=80−−

  a =  √80

a=80−−

3. Examples of the Pythagorean Theorem

When you use the Pythagorean theorem, just remember about hypotenuse  . Look at the following examples to see pictures of the formula.

4. Solving the Hypotenuse

    Use the Pythagorean theorem to determine the length of X

a=80−−80−−√

 Step 1) Identify the legs and the hypotenuse of the right triangle. 

•   The legs have length '6 and '8' . 'X' is the hypotenuse because it is opposite the right angle. 

Step 2) Substitute values into the formula  A² + B² = C²

• 6² + 8² = X² 

Step 3) Solve for the unknown

 

4. Solving the Pythagoras Theorem

^{Use the Pythagorean theorem to calculate the value of X. Round your answer to the nearest hundredth.}

^{Remember our steps for how to use this theorem. This problems is like question 4 above.}

^{Step 1) Identify the legs and the hypotenuse of the right triangle.}

^{The legs have length '10' and 'X'. The hypotenuse is 20.}  

^{Step 2) Substitute values into the formula (remember 'c' is the hypotenuse)}

^{A2 + B2 = C2
102 + X2 = 202}

^{Step 3 ) Solve for the unknown}

    

Pythagoras Theorem

Pythagoras Theorem

• In a right angled triangle the square of the long side is equal to the sum of the squares of the other two sides.
  
  
  
  It is stated in this formula:
  
  
  If we know the lengths of two sides of a right angled triangle, we can find the length of the third side. (But remember it only works on right angled triangles!) 
• Note:  
• a is the longest side of the triangle 
•   b and c are the other two sides
  
  
  
  
  There are certain sets of numbers that have a very special property in relation to the Pythagorean Theorem.  Not only do these numbers satisfy the Pythagorean Theorem, but any multiples of these numbers also satisfy the Pythagorean Theorem.  
  
  
  
  

  

  For example:  the numbers 3, 4, and 5 satisfy the Pythagorean Theorem.  If you multiply all three numbers by 2  (6, 8, and 10), these new numbers ALSO satisfy the Pythagorean theorem.  
    The special sets of numbers that possess this property are called
  Pythagorean Triples.
  
  
  The most common Pythagorean Triples are:
  3, 4, 5
  5, 12, 13
  8, 15, 17

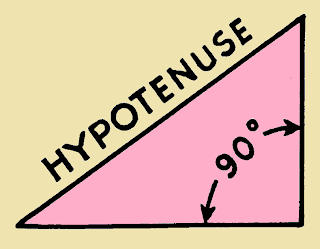
Hypotenuse

What is Hypotenuse?

•  Hypotenuse is the longest side of the triangle.

•  Hypotenuse is the side opposite the right angle in a right angled triangle. 

Determine the Hypotenuse

From this figure, we can see that c is the side opposite right angle.

So,  C = HYPOTENUSE 



Calculate the Hypotenuse


Look at the triangle below.

We want to find the length of the hypotenuse (h).

 Pythagoras' Theorem tells us:

 The square of the hypotenuse is equal to the sum of the squares of the two shorter sides.
In this case, this means that h² is equal to 5² + 12².

So the length of the hypotenuse (h) can be worked out as follows:

h² = 5² + 12²    ( work out the squares of the two shorter side )
h² = 25 + 144   (add the squares of the two shorter sides together )
h² = 169           ( square root both sides to find the value of h)
h  = 13

We can now see that the length of the hypotenuse (h) is 13m.